Merge sort je algoritmus, založený na tzv. principu rozděl a panuj (latinsky divide et impera, anglicky divide and conquer). To znamená, že pokud nějaký problém neumíme vyřešit v celku, rozložíme si ho na více menších a jednodušších problémů. Ten samý postup aplikujeme i na tyto problémy (opět je rozdělíme na ještě menší, mimochodem velmi se zde nabízí rekurzivní řešení) až se dostaneme na takovou úroveň, kterou jsme schopni bez problému řešit. V problému třídění se často chceme dostat až k poli velikosti 1, které považujeme automaticky za setříděné.
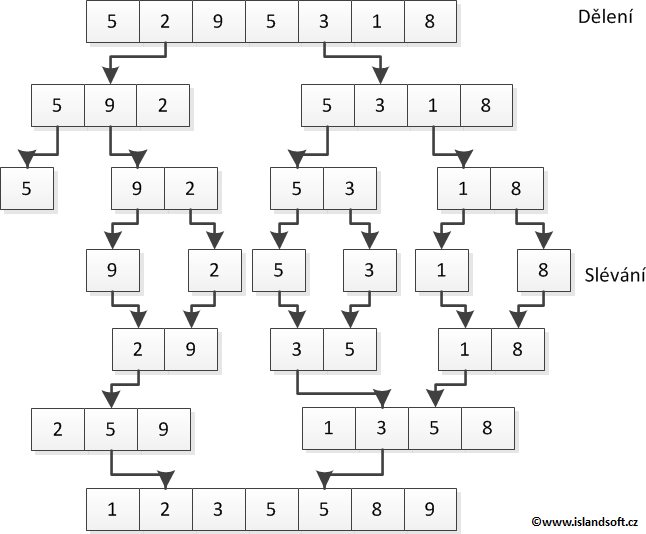
Merge sort operuje s myšlenkou, že dokážeme velmi rychle a v lineárním čase slít (spojit, anglicky merge)dvě již setříděná pole do jednoho tak, aby výsledné pole bylo opět setříděné. Na začátku samozřejmě máme jen jedno pole a to setříděné není. My si ho však můžeme rekurzivně rozdělit na 2 poloviny, každou polovinu opět rozdělit na další poloviny a tak dále. V nejhlubší hladině rekurze se nutně dostaneme do fáze, kdy nám zbydou už jen samá jednoprvková pole. Jednoprvkové pole můžeme považovat za setříděné, říká se o něm, že je setříděné triviálně. Jak se postupně vynořujeme z rekurze, sléváme tato jednoprvková pole na dvouprvková, ta na čtyřprvková a tak pokračujeme, dokud nám nezbydou dvě velká pole, která když slijeme, dostaneme naše původní pole setříděné. Protože sléváme vždy po rozdělení na poloviny, budeme to jistě dělat log n krát (kde základem logaritmu je 2, protože dělíme na 2 poloviny). Samotné slévání zvládneme v čase O(n), výsledná časová složitost algoritmu tedy bude O(n log n). Nejprve si ukážeme, jak se pole slévají.

    public static void MergeSort(int[] data, int start = 0, int end = -1)
        {
            if (end < 0)
                end = data.Length;

            if (start + 1 >= end)
                return;

            int mid = (start + end) / 2;

            MergeSort(data, start, mid);
            MergeSort(data, mid, end);

            int[] tmp = new int[end - start];
            int i = 0;

            int l = start;
            int r = mid;

            while (l < mid && r < end)
            {
                if (data[l] <= data[r])
                    tmp[i++] = data[l++];
                else
                    tmp[i++] = data[r++];
            }

            while (l < mid)
            {
                tmp[i++] = data[l++];
            }

            while (r < end)
            {
                tmp[i++] = data[r++];
            }

            for (int x = 0; x < tmp.Length; x++)
            {
                data[start + x] = tmp[x];
            }
        }