Programování
Heap sort
Heapsort patří mezi chytré algoritmy, které jsou řádově rychlejší
než ty doposud zmíněné. Staví na myšlenkách algoritmu Selection
sort a je tedy založený na odtrhávání extrému (v tomto případě
maxima), které vždy přesouvá na konec pole. Po začlenění všech maxim na
konec máme jistě pole setříděné. Problém Selection sortu však byl
právě ve hledání maxima nebo minima. V každém vnějším cyklu se celá
nesetříděná část pole musela projet a každý prvek zkontrolovat, zda
není náhodou hledaným maximem. V poli maximum rychleji asi nenalezneme.
Ale co kdyby existovala datová struktura, ve které bychom mohli prvky reprezentovat stejně, jako v poli, a zároveň jsme maximum nalezli v konstantním čase , bez jediného průchodu? Když se takto ptám, asi vám je již jasné, že struktura existovat bude. Nazývá se Halda (anglicky Heap, proto Heap sort neboli třídění haldou).
Halda je binárním stromem s následujícími vlastnostmi:
Halda může vypadat například takto:
Ale co kdyby existovala datová struktura, ve které bychom mohli prvky reprezentovat stejně, jako v poli, a zároveň jsme maximum nalezli v konstantním čase , bez jediného průchodu? Když se takto ptám, asi vám je již jasné, že struktura existovat bude. Nazývá se Halda (anglicky Heap, proto Heap sort neboli třídění haldou).
Halda je binárním stromem s následujícími vlastnostmi:
- Všechna "patra" haldy až na poslední jsou plně obsazeny prvky (tedy každý vnitřní vrchol má právě 2 syny, strom je velmi vyvážený)
- Poslední patro haldy je zaplněno zleva (může být i zaplněno celé)
- Pro prvky v haldě platí tzv.speciální vlastnost haldy: oba synové jsou vždy menší nebo rovny otci.
Halda může vypadat například takto:
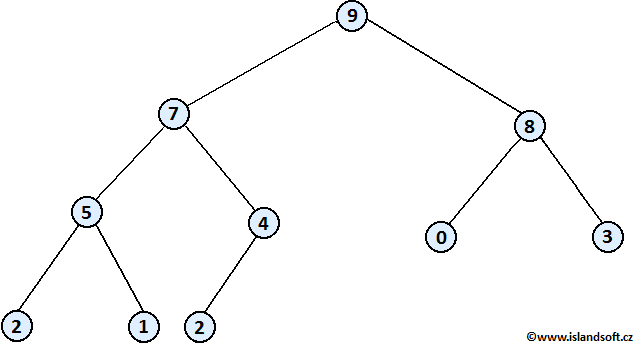
Samozřejmě si můžeme definovat speciální vlastnost haldy obráceně a
mít v kořeni minimum, i to se používá.
Protože obvykle chceme třídit pole a ne haldu, musíme si z tohoto pole haldu nejprve postavit. Teď jistě očekáváte, že si vytvoříme stromovou strukturu pomocí ukazatelů nebo referencí a do ní budeme prvky přidávat. Haldu lze však malým trikem (díky jejímu vyvážení) reprezentovat v obyčejném poli, nebudeme tedy potřebovat žádnou pomocnou strukturu ani paměť. Budeme pracovat přímo v našem poli, na které se budeme dívat jako na haldu a můžeme tedy třídit rovnou na místě.
Halda v obrázku výše by v poli vypadala takto (nahoře indexy prvků, dole prvky):
Všimněte si, že zhaldované pole nemá moc společného s polem
setříděným. Teď si ukážeme, jak s tímto polem pracovat jako s haldou.
Jistě jste si všimli, že prvky v poli jsou prvky tak, jak jsou v haldě,
seřazené shora dolů a zleva doprava. Když budeme chtít přistoupit ke
kořeni, jednoduše sáhneme na index 0, poslední prvek haldy je také na
indexu posledního prvku pole. Budeme však potřebovat přístup z libovolného
otce do jeho synů a také ze syna k jeho otci.
Pokud bude mít syn index i, index jeho otce vypočítáme jako (i - 1) / 2 (dělení je celočíselné). Pokud bude mít otec index i, jeho levý syn bude mít index (2 * i + 1) a pravý syn (2 * i) + 2.
Můžeme si rychle ověřit, že to funguje. Zkusíme najít syna prvku 7, ten má index 1 (pole je indexováno od 0 a je druhý). (1 - 1) / 2 je 0, jeho otec je tedy prvek 9, což sedí. Jeho synové budou (2 * 1 + 1) = 3 a na třetím indexu je pětka - opravdu jeho levý syn. Pravý syn má index o jednu větší a opravdu je na něm prvek 4.
Máme tedy potřebné nástroje a můžeme se pustit do prvního kroku algoritmu - zhaldování pole.
Protože obvykle chceme třídit pole a ne haldu, musíme si z tohoto pole haldu nejprve postavit. Teď jistě očekáváte, že si vytvoříme stromovou strukturu pomocí ukazatelů nebo referencí a do ní budeme prvky přidávat. Haldu lze však malým trikem (díky jejímu vyvážení) reprezentovat v obyčejném poli, nebudeme tedy potřebovat žádnou pomocnou strukturu ani paměť. Budeme pracovat přímo v našem poli, na které se budeme dívat jako na haldu a můžeme tedy třídit rovnou na místě.
Halda v obrázku výše by v poli vypadala takto (nahoře indexy prvků, dole prvky):
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 9 | 7 | 8 | 5 | 4 | 0 | 3 | 2 | 1 | 2 |
Pokud bude mít syn index i, index jeho otce vypočítáme jako (i - 1) / 2 (dělení je celočíselné). Pokud bude mít otec index i, jeho levý syn bude mít index (2 * i + 1) a pravý syn (2 * i) + 2.
Můžeme si rychle ověřit, že to funguje. Zkusíme najít syna prvku 7, ten má index 1 (pole je indexováno od 0 a je druhý). (1 - 1) / 2 je 0, jeho otec je tedy prvek 9, což sedí. Jeho synové budou (2 * 1 + 1) = 3 a na třetím indexu je pětka - opravdu jeho levý syn. Pravý syn má index o jednu větší a opravdu je na něm prvek 4.
Máme tedy potřebné nástroje a můžeme se pustit do prvního kroku algoritmu - zhaldování pole.
Není Stabilní
Na místě
O (n log n)
Rychlý
Omicron: n log n
Omega: n log n
Theta: n log n
Průběh
Máme pole následujících prvků:
Pole nám reprezentuje následující "haldu":
| 3 | 2 | 5 | 1 | 9 | 4 |
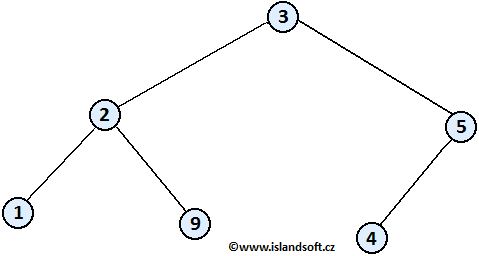
Uvozovky jsem použil záměrně, protože tato halda je rozbitá - neplatí
nám speciální vlastnost haldy. Musíme ji tedy opravit a pole zhaldovat.
Použijeme k tomu funkci up (nahoru), kterou budeme postupně
volat na prvky od kořene dolů. Funkce zjistí, jestli daný prvek neporušuje
speciální vlastnost haldy (tedy pokud není větší než jeho otec) a pokud
je, prvek s otcem prohodí. Tím se však může stát, že se stejný problém
přenese o úroveň výše, proto se funkce opakuje, dokud speciální vlastnost
haldy pro daný prvek neplatí nebo dokud nedojedeme do kořene. Funkci voláme
pro každý prvek dokud nedojedeme nakonec, pak si můžeme být jisti, že jsme
haldu opravili.
Z důvodu úspory místa v článku jen popíši průběh zhaldování,
dívejte se přitom na obrázek výše. Můžete se také podívat na video
níže, kde je to podrobně znázorněno.
Na první prvek (kořen, 3) funkci up pouštět nebudeme, protože ten
žádného otce nemá. Začneme tedy s prvkem 2, ten je menší než otec,
necháme ho na místě. Další je prvek 5, ten je větší než otec (3), proto
ho s otcem prohodíme a jsme již v kořeni, takže končíme. Prvek 1 je
menší než 2, to je v pořádku. 9 je však větší než 2, proto je
prohodíme. 9 je však stále větší než 3, prohodíme tedy znovu a 9
(maximum) se dostává do kořene. 4 je větší než 3, proto prohodíme. 4 je
potom menší než 9, to je již v pořádku. Zhaldované pole a halda, kterou
reprezentuje, vypadají následovně:
| 9 | 5 | 4 | 1 | 2 | 3 |
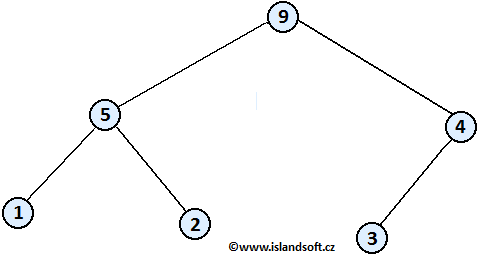 Neni hotovo = malo času
Neni hotovo = malo času
Kod
public static void HeapSort(int[] data)
{
// build heap
for (int i = data.Length - 1; i >= 0; i--)
{
RepairTop(data, i, data.Length);
}
// sort
for (int i = data.Length - 1; i > 0; i--)
{
Swap(0, i, data);
RepairTop(data, 0, i);
}
}
public static void RepairTop(int[] data, int top, int max)
{
int l = top * 2 + 1;
int r = top * 2 + 2;
if (l >= max)
return;
int can = (r >= max || data[l] > data[r]) ? l : r;
if (data[can] > data[top])
{
Swap(top, can, data);
RepairTop(data, can, max);
}
}
public static void Swap(int a, int b, int[] data)
{
int tmp = data[a];
data[a] = data[b];
data[b] = tmp;
}
Video
Zdroj: Video Link