Rekurze je programovací technika, při níž je určitá procedura nebo funkce znovu volána dříve, než je dokončeno její předchozí volání.

Použití rekurze může u některých úloh vést ke stručnému a matematicky elegantnímu řešení. Nevede ale nutně k řešení optimálnímu. Použití rekurze vede obvykle k jinému rozložení využití prostředků přidělených programu operačním systémem, případně k jejich rychlejšímu vyčerpání, proto se při optimalizaci programu většinou snažíme rekurzi omezit nebo odstranit.

Rekurzi nepoužíváme pro úlohy, které jdou snadno vyřešit prostým cyklem.

Některé (zejména starší) programovací jazyky a některé překladače rekurzi neumožňují; jiné vyžadují, aby programátor explicitně uvedl, že je daná procedura nebo funkce rekurzivní.

Řadu rekurzívních algoritmů lze nahradit iteračními, které počítají výsledek „zdola nahoru“, tj, od menších (jednodušších) dat k větším (složitějším)
Vše co jde napsat rekurzivně, jde i iterativně !

Výhodou rekurzivních funkcí (procedur) je jednoduchost a přehlednost
Nevýhodou může být časová náročnost způsobená např. zbytečným opakováním výpočtu

Volání může probíhat přímo nebo nepřímo:

• Přímá rekurze nastává, když podprogram volá přímo sám sebe.
• Nepřímá rekurze je situace, kdy vzájemné volání podprogramů vytvoří „kruh“. Např. ve funkci A se volá funkce B a ve funkci B se volá opět funkce A.

Podprogram může být volán jednou nebo vícekrát:

• Lineární rekurze nastává, pokud podprogram při vykonávání svého úkolu volá sama sebe pouze jednou. Vytváří se takto lineární struktura postupně volaných podprogramů.
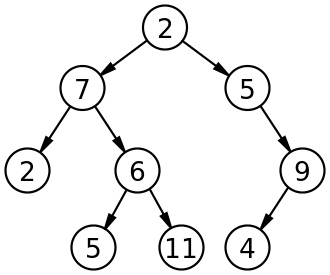
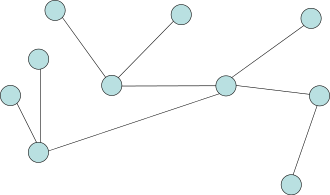
• Stromová rekurze nastává, pokud se funkce nebo procedura v rámci jednoho vykonání svého úkolu vyvolá vícekrát. Strukturu volání je možné znázornit jako zakořeněný strom . Pro dvě volání v jednom průchodu vzniká binární strom , pro tři ternární strom, atd. (Počet rekurzivních volání nemusí být konstantní, např. při rekurzivním procházení grafu voláme zpracování na všechny sousedy vrcholu, a těch je obecně různý počet.)

Program, který používá rekurzivní volání, obvykle provádí tyto kroky:

• Kontrola
• Inicializace
• Vlastní rekurze
  • Rozdělení problému na dílčí podproblémy.
  • Zavolání funkcí, které řeší daný podproblém (tady nastává přímé nebo nepřímé volání sebe sama).
  • Sestavení výsledku.
• Vrácení výsledku.

V oblasti algoritmů můžeme pomocí rekurze nalézt řešení obecných úloh rozkladem na dílčí úlohy stejného typu. Často jej nalezneme v algoritmech typu „rozděl a panuj“. Tato programovací technika se hodí pro takové úlohy, u nichž je rozdělení na menší úlohy stejného charakteru snadné a přirozené. Typickým příkladem přirozeně rekurzivního algoritmu je průchod stromem (s obecným počtem potomků):

    
        int fakt_rek(int number) 
        {
            if (number < 0)
            {
                return 0;
            }

            if (number == 0 || number == 1)
            {
                return 1;
            }

            return number * fakt_rek(number - 1);
        }